【はじめに】量子もつれとは?簡単にわかりやすく言うと…

さて、今日は『量子もつれ(Quantum Entanglement)』について話してみようか。

えっ?もつれ?髪の毛が寝ぐせでからまってるみたいなやつですか?

…例えとしては意外と悪くない。が、量子の世界では“とんでもなく不思議な”もつれ方をするんじゃよ。
量子もつれとは、量子の世界の“つながり”!?

量子もつれとは、2つの粒子が、たとえどれだけ遠くに離れていても、まるで一心同体のように振る舞う現象です。
たとえば、1つの光子の性質を測定すると、もう片方の光子の性質が即座に決まってしまう──そんな相関関係が観測されます。

えっ?そんなことが!片方を測ったら、もう片方の情報もわかっちゃうなんて!

その驚きこそ、量子もつれの核心なんだ。しかも、どれだけ遠くにあってもだよ。100kmでも、月でも、理論的には銀河の端でもね。
簡単にたとえるなら…
「赤と青のビー玉」が入った箱を想像してみてください。
2人で1個ずつ持って、離れた場所で開けると、どちらかは赤・もう一方は青になります。
でもこの場合は最初から決まっていた色が入っていただけですよね。
ところが量子もつれでは、開けてみるまで色が決まっていないのに、開けた瞬間にもう片方の色も決まってしまうような振る舞いをします。

つまり、測定という“行為”によって、同時に2つの結果が確定する。これが古典的な世界とは決定的に違うんだ。

うう、ちょっとゾワッとしました…。これ、怖くないですか?
何がそんなに不思議なの?
量子もつれが不思議なのは、次のようなポイントです:
- 物理的に接触していなくても、強い相関が生じる
- 測定前は、それぞれの粒子が「どんな状態か」は決まっていない
- 測定した瞬間、相手の状態も決まってしまう
- しかもこれは、ランダムなふるまいなのに統計的には完璧に一致する

博士、それってつまり…“心がつながってる”とか“量子テレパシー”とか、そんな話なんですか?

いい線いっておる。実際、一部では“不気味な遠隔作用”なんて呼ばれていたくらいじゃ。
本記事のテーマ
この記事では、この不思議な現象をめぐって物理学者たちがどんな議論をし、どんな実験で確かめてきたのか、そしてどうやってこの「もつれ」を人工的に作るのかを、順を追って解説していきます。
1. 量子もつれとは?仕組みをやさしく解説

博士、さっき“離れていてもつながってる”って聞いたときは驚いたけど…どうしてそんなことが起こるんですか?仕組みが全然わからなくて…

お、それは良い質問じゃ。じゃあ今回は、“量子もつれ”の仕組みをもう少し本格的に、でもやさしく解説してみよう。
量子もつれとは?定義をやさしく言い直すと…
量子もつれとは、2つ以上の量子が、それぞれをバラバラに扱えないほど強く結びついている状態のことです。
一方の粒子に何かが起きると、もう片方にも即座に影響が現れるという不思議な性質を持ちます。
たとえば、もつれた光子AとBがあるとします。Aを観測した瞬間に、その結果に応じてBの状態も決まってしまいます。
しかもこの現象は、たとえ両者が何キロ離れていても成立するのです。
量子状態ってどう表すの?
量子もつれを理解するには、「量子状態の記号」に少しだけ慣れる必要があります。
量子力学では、以下のような記号がよく使われます:
- \(
\left| 0 \right\rangle
\)(読み方:けっと・ぜろ)… 量子ビットの状態「0」 - \(
\left| 1 \right\rangle
\)(けっと・いち)… 状態「1」 - \(
\left| \psi \right\rangle \
\)(けっと・ぷさい)… ある量子状態全体を表す一般的な記号
これらは、量子ビット(qubit)の基本状態で、古典的には「オン・オフ」ですが、量子では「両方が重なった状態」も許されます。
たとえば以下のように:
\left| \psi \right\rangle = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle
\)
ここで \(\alpha\) と \(\beta\) は複素数で、\(
|\alpha|^2 + |\beta|^2 = 1 \
\)(確率の合計)になります。
2つの粒子が「1つの全体」になる:量子もつれの数式的な形
量子もつれの代表的な例が ベル状態(Bell states) と呼ばれるものです。
最も有名な例はこちら:
\left| \Phi^+ \right\rangle = \frac{1}{\sqrt{2}} \left( \left| 0 \right\rangle_A \left| 0 \right\rangle_B + \left| 1 \right\rangle_A \left| 1 \right\rangle_B \right) \
\)
これは、「AもBも0」か「AもBも1」のどちらかになっている、という状態です。

えっ、それってAとBが“同じ結果になる”ってことですか?

その通り。しかも、測定するまでは“どちらでもある”状態なんじゃ。
つまり、それぞれの粒子を単独で観測すると、測定結果は完全にランダム(例えば50%の確率で縦または横の偏光)に見えます。ところが、どちらかの粒子を測定すると、もう1つの粒子は必ず同じ結果(または必ず反対の結果)になるという強い相関が見られるのです。
このように「片方だけを見ても何も決まっていないように見える」のに、「2つを比べると確実にパターンがある」――それが量子もつれの不思議な特徴です。
古典的な相関とどう違うの?
ここで大事なのは、「量子もつれによる相関」と「古典的な相関」は本質的に異なるということです。
| 種類 | 内容 |
|---|---|
| 古典的相関 | 例:赤いビー玉と青いビー玉を袋に入れて、1人ずつ取り出す。どちらかが赤なら、もう片方は青になる。でも最初から色は決まっている。 |
| 量子もつれの相関 | 測るまでどちらの色か決まっていないのに、測定した瞬間にもう一方の結果も確定する。しかも統計的に完璧に一致する。 |
量子もつれでは、事前に結果が「隠れている」のではなく、測定によって状態が生まれると考えられているのです。

だから、いくら事前に調べても、測定するまでは結果は未定。まるで“現実が測定によって作られる”かのようだとさえ言われているんだよ。
量子もつれの仕組みまとめ:なぜそんなことが起こるのか?
量子もつれが起こる根本的な理由は、量子力学における「重ね合わせ」と「非局所的な相関」が可能だからです。
- もつれ状態の各粒子は「0」と「1」の両方を同時に持つ(重ね合わせ状態)
- 測定結果は確率的であるが、相関が完璧に現れる
- つまり、片方だけでは意味がなく、2つ合わせて初めて状態の全体像が見える

うーん……なんか、見えない糸でつながってる感じですね。測った瞬間に、“答えが一緒”って決まるみたいな?

その“見えない糸”こそが、量子もつれの本質なんじゃ。しかもその糸は、情報を運ばずに、結果だけを一致させる……不思議な関係なんじゃよ。
次は「なぜこの仕組みが問題視されたのか」を見てみよう
量子もつれの仕組みは、一見“魔法”のように思えるかもしれません。
実際、アインシュタインたちはこれを「不完全な理論だ」と批判しました。
次章では、「EPRパラドックス」と呼ばれるこの問題提起から、量子もつれの“正体”を暴こうとした科学者たちの議論を紹介していきます。
2. 量子もつれの歴史:EPRパラドックスから実験的検証まで

博士、量子もつれって未来のテクノロジーってイメージですけど、けっこう昔から議論されてたって本当ですか?

本当だよ。量子もつれの議論は1935年までさかのぼるんだ。アインシュタインたちが発表した論文、「EPR論文」がその始まりだよ。
2-1. アインシュタインたちが唱えた「EPRパラドックス」とは?

EPR論文とは?
1935年、アインシュタイン、ポドルスキー、ローゼンの3人は、「量子力学は本当に完全な理論なのか?」という問いを提起する論文を発表しました。それが後に「EPRパラドックス」と呼ばれるものです。
この論文では、以下のような問いが立てられました:
「ある粒子の状態を観測することで、遠く離れたもう一つの粒子の状態が即座にわかるとしたら、それは物理的におかしいのでは?」
量子もつれと「同時に決まる」不思議
たとえば、ある1つの粒子が2つに分かれて、遠く離れた2人がそれぞれ1つずつ持っていたとします。
そして、どちらかが一方の粒子を測定したとたん、もう一方の粒子の結果も瞬時に決まってしまうように見える。
このような現象を、当時の物理学では説明できませんでした。
アインシュタインが信じていた「局所実在論」
アインシュタインはこの奇妙な現象に納得がいかず、「何か隠された情報(変数)があるはずだ」と主張しました。
この考え方は「局所実在論」と呼ばれます。
- 実在性(Realism):観測していなくても物理量は決まって存在している
- 局所性(Locality):離れた場所には瞬時に影響を与えられない(情報の伝達は光速以下)
この考えに基づけば、「離れた粒子が一瞬で影響し合う」なんてことはあり得ないはず。
アインシュタインは、この量子もつれの振る舞いを「spooky action at a distance(遠隔での不気味な作用)」と呼んで批判しました。

つまり、「もつれた粒子が瞬時に連動するのはおかしい。だから裏に何か仕掛けがあるはず」って主張だったわけですね。

そう。アインシュタインたちは「量子力学は統計的には当たるけど、実際には何か“隠された変数”があって、それがこの奇妙な相関を説明している」と考えていたんじゃよ。
EPRパラドックスが残した問い
EPR論文が投げかけたのは、次のような根本的な問いです:
- 「物理的実在とは何か?」
- 「私たちの観測はどこまで影響を与えているのか?」
- 「量子力学は完全な理論なのか、それともより深い理論があるのか?」
この問いは、その後数十年にわたって物理学者たちを悩ませ続けました。そして、20世紀後半に、ある人物がこのパズルに一つの理論的回答を与えます。
このセクションのまとめ:
| 用語 | 解説 |
|---|---|
| EPR論文 | 1935年にアインシュタインたちが提起。「量子力学は不完全かもしれない」と主張 |
| 局所実在論 | 観測しなくても物理量は決まっていて、遠隔地には瞬時に影響しないという考え方 |
| Spooky Action | 量子もつれによって「遠く離れた粒子が同時に状態を決める」ことへの批判的表現 |
| パラドックス | 現象と理論の矛盾によって生じた深い問い。「本当にこの世界はそうなっているのか?」 |
2-2. ベルの不等式とその破れが意味するもの
~アインシュタインの疑問に挑んだ理論とその衝撃的な結論~

博士、EPR論文では「量子力学は不完全だ」ってアインシュタインが言ったんですよね。でもその後、誰かがそれを検証しようとしたんですか?

その通り。1964年にジョン・ベルという物理学者が登場して、EPRパラドックスの核心に数学的な形で迫ったんだ。それが有名な「ベルの不等式」じゃよ。
ベルの不等式とは?:局所実在論の検証ツール
ベルは、「もし局所実在論(EPRの立場)が正しければ、粒子同士の相関にはある数学的不等式が成り立つはずだ」と示しました。それが「ベルの不等式」です。
一方で、量子力学の予測はその不等式を破るような結果になるのです。
つまり:
| 条件 | 成り立つこと |
|---|---|
| 局所実在論が正しい | ベルの不等式は常に満たされる |
| 量子力学が正しい | 状況によってベルの不等式が破れることがある |
ベルの不等式の核心(イメージ解説)
モソッティと博士がもつれた粒子の測定実験をするとしましょう。
- モソッティがA地点で粒子のスピンを測定
- 博士がB地点で別の粒子のスピンを測定(この2つはもつれたペア)
局所実在論に基づけば、AとBの測定結果の相関はある一定の範囲に収まるはずです(これが不等式)。
でも、量子力学の予測では、この相関がその範囲を超えてしまうのです。

これは単なる理論の話じゃなくて、実際に量子力学の計算結果と局所実在論の予測が食い違う点があることを数学的に示したんじゃ。つまり、「どちらかは間違っている」ということを証明したわけだね。

えっ、それって「アインシュタインの直感」か「量子力学の計算」か、どちらかが間違ってるってことですか!?

そうじゃ。ジョン・ベルは、量子力学の不思議な相関がただの「見かけの問題」ではなく、現実の性質そのものを問う問題だと明らかにしたんじゃよ。
では実験ではどうだったのか?
ベルの不等式は単なる理論式ではありません。実際にこれを実験で検証することが可能です。
この章の次で紹介するように、1980年代からさまざまな物理学者が「ベルの不等式を破るかどうか」の実験に取り組みました。
- 単なる統計的な相関では説明できない相関が現れる
- 隠れた変数ではなく、量子力学的な非局所性によって説明される
- 「遠く離れた粒子の状態が、一瞬でつながっている」ように見える(=非局所的)
このセクションのまとめ
| 用語 | 解説 |
|---|---|
| ベルの不等式 | 局所実在論が正しければ成り立つはずの数学的不等式 |
| 不等式の破れ | 実験が量子力学の予測どおりになり、局所実在論が否定される |
| 非局所性 | 空間的に離れていても粒子同士が瞬時に影響し合っているように見える性質 |
| 意義 | 量子力学が単なる理論ではなく、現実の描写であることを示す重要な証拠 |
3-3. 実験で本当に確認されたのか?
~ベルの不等式を破る「決定的な証拠」は得られたのか~

博士、ベルの不等式が理論的に破れるって話はわかりました。でも、それって本当に実験で確かめられてるんですか?

いい質問だね。実はこの問いに物理学者たちは何十年もかけて挑戦してきたんだよ。そして今では、もつれの存在は「実験的事実」だと広く認められているんじゃ。
1981年:アラン・アスペの歴史的な実験
フランスの物理学者アラン・アスペは1981年から1982年にかけて、量子もつれを利用してベルの不等式を破る実験を行いました。
- 非線形光学結晶を使って、もつれた光子のペアを作成
- 光子ペアを別々の場所へ飛ばし、それぞれの偏光を測定
- 測定の角度をランダムに変え、相関を統計的に取得
➡ ベルの不等式は破られ、量子力学の予測どおりの結果が得られた。

うわー、それって「アインシュタインの局所実在論」が実験で否定されたってことですか?

厳密に言うとこの段階では、アスペの実験にはまだ「抜け穴(loophole)」と呼ばれる問題が残っていたんじゃ。
たとえば:
- 検出効率の問題(光子を検出できない場合が多い)
- 測定タイミングの問題(設定変更のタイミングが不十分)
こうした「抜け穴」があると、量子力学以外の説明も可能になる余地が残ってしまう。
2015年:抜け穴なし実験(loophole-free Bell test)
2015年、オランダのデルフト工科大学など複数の研究機関が、「抜け穴のない」ベル実験に成功しました。
- 測定装置の設定変更が完全にランダムで速い
- 検出効率も十分に高く、測定漏れが少ない
- 測定地点が空間的に独立している(光速でも情報が届かない)
➡ 再びベルの不等式は破られた。
これにより、量子もつれは実在し、「非局所性」は避けられないとされるようになったのです。
もはや量子もつれは「疑いようのない現象」
- 世界中で複数の研究チームがベルの不等式破れを再現
- 光子、イオン、原子、超伝導回路など多様なシステムで確認
- 現在では、もつれを使った量子暗号・量子通信が実用段階に

つまり、もつれっていうのは理論だけじゃなくて、本当に起きてる現象なんですね!

そのとおり。もつれは自然界の本質的な振る舞いなんじゃ。そしてそれは、人間の直感とはまったく違うルールで動いている。そこが面白いところなんじゃよ。
このセクションのまとめ
| トピック | 内容 |
|---|---|
| アスペの実験 | 1981年にベルの不等式が初めて破られた実験。だが抜け穴あり。 |
| 抜け穴なし実験 | 2015年以降、検出効率・空間分離・タイミングの条件をクリア |
| 結論 | 量子もつれは実験的に確認された物理現象である |
3.どうやって量子もつれを作るのか?
~光子、原子、超伝導回路での生成方法をやさしく解説~

博士、前の章で「量子もつれは実在する」って分かりました。でも…それって、どうやって作ってるんですか?魔法ですか?

魔法じゃない、ちゃんとした物理じゃ(笑)。いくつか代表的な方法があるから、順に見ていこう!
3-1. 光子でもつれを作る:SPDC(自発的パラメトリック下方変換)
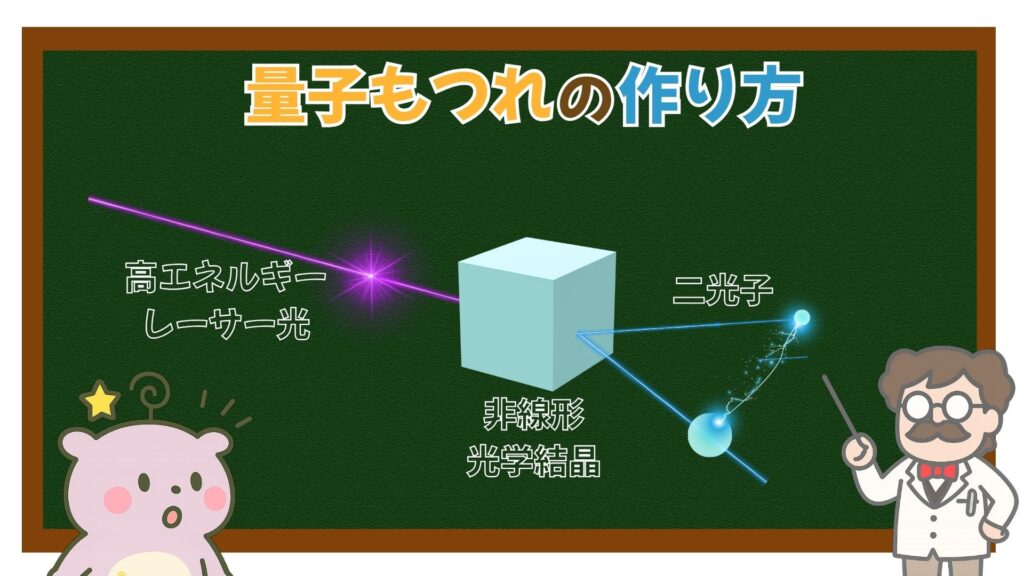
量子もつれを作る最も一般的な方法が、光子(フォトン)を使った手法です。
仕組み(ざっくり説明)
- 高エネルギーのレーザー光(紫外線など)を
- 非線形光学結晶(BBO結晶など)に照射すると
- 光が2つの低エネルギー光子に分裂します
これを「自発的パラメトリック下方変換(SPDC)」と呼びます。
- 2つの光子(A, B)は、偏光や運動量などで強く相関
- その相関が量子もつれの状態を表す
- SPDCは「確率的」にしか起きないが、現代の装置では十分な頻度で生成可能

へぇー!光が分裂して、もつれたペアになるんですね!
3-2. 測定可能な形に整えるための光学系
もつれた状態を作り・測定するには、以下のような光学機器が用いられます:
- 非線形結晶(SPDC用):1つの光子から2つのもつれた光子を生成
- サニャック干渉計:光の経路と干渉を制御し、状態の作成や安定化に利用
- ビームスプリッター、偏光子、波長板:測定軸の選択やランダム性の導入に利用
これらの装置を組み合わせることで、高精度な量子もつれ実験が可能になります。
3-3. 光子以外でも:イオン・原子・超伝導回路
イオントラップ方式(量子コンピュータで使われる)
- 電場で原子(イオン)を空中に浮かせ、レーザーで操作
- 2つのイオンを共鳴操作(共通の振動)でもつれさせる
固体量子ビット(超伝導回路)
- ジョセフソン接合を使った人工原子
- 回路内の量子ビット同士をマイクロ波で結合し、もつれを生成

光だけじゃなくて、イオンとか回路でももつれを作れるんですね!

そう。しかも、これらの技術はすでに量子コンピュータや量子通信の中核として実用化が進んでいるんだよ。
このセクションのまとめ
| 方法 | 概要 | 特徴 |
|---|---|---|
| SPDC | 光子を非線形結晶で分裂させる | 実験が比較的簡単で再現性が高い |
| 干渉計 | 光子の経路を制御して測定精度を向上 | 光学実験の定番手法 |
| イオントラップ | レーザーで冷却・操作したイオンを共鳴させる | 量子コンピュータに応用中 |
| 超伝導回路 | マイクロ波で回路中の量子ビットをもつれさせる | 高速処理・安定性が向上中 |
4.まとめ:量子もつれが示す新しい世界の可能性
量子もつれは、直感では理解しづらい「離れた粒子が一体化したように振る舞う」という現象です。けれど、それはただの奇妙な物理現象ではありません。量子もつれは、未来の技術の中核を担う「現実に活用できる資源」なのです。
もはや仮説ではなく「確立された事実」
アインシュタインが疑問を呈し、ベルの不等式で理論的に検証され、さらに現代の実験で何度も確認されてきた量子もつれ。
この現象は「現実に存在する」ことが、科学的に確立されました。
つまり、「粒子が離れていても一体のように振る舞う」「測定結果が瞬時に関連しあう」といった非局所的な性質が、自然界に本当にあるということです。
私たちが慣れ親しんでいる「古典的な世界観(原因と結果は隣接して伝わる)」が、量子レベルでは通用しない場面があると分かったのです。
技術応用という次のステージへ
量子もつれは、すでに次のような技術へと応用が進んでいます:
- 量子暗号通信
もつれた光子の測定結果を比較することで、盗聴を検知できる。絶対に安全な通信が理論的に可能。 - 量子テレポーテーション
「もつれた粒子対」を利用し、量子状態(情報)を元の場所から消して、別の場所に再構築する技術。
ただし、再構築には古典通信が必要なので、情報が光速を超えて瞬時に伝わるわけではありません。 - 量子コンピュータ
複数の量子ビットをもつれさせることで、並列的な演算が可能に。従来型コンピュータでは不可能な問題を解ける可能性がある。
「現実は非局所的かもしれない」というインパクト
量子もつれの存在は、私たちの「世界観」を根本から揺さぶります。
- 実際に離れていても、何らかの情報的なつながりが存在する
- そのつながりは、私たちの空間的・時間的な常識を超えている
このような量子世界の性質は、「宇宙の本質はどうなっているのか?」という深い問いに対して、これまでにないヒントを与えてくれるかもしれません。
量子もつれは、「奇妙さ」から「基盤技術」へ
量子もつれは、かつてはただの謎やパラドックスとして扱われていました。
しかし今では、実験で確認され、応用技術の中核にもなる、極めてリアルな現象です。
この不思議な量子の世界を理解し、活用することで、私たちは未来の通信・計算・安全保障の在り方を変えていくことができるのです。
5. よくある質問(FAQ)
Q1. 量子もつれはなぜそんなに不思議だと言われるの?
A:
量子もつれが不思議とされる理由は、「離れた場所にいる2つの粒子が、まるで1つの存在のように連動している」ように見えるからです。しかも、それが瞬時に起こるように見えるのです。
アインシュタインはこれを「遠隔作用(spooky action at a distance)」と呼び、直感に反すると感じました。普通の常識(例:手紙や光の通信)では、何かが影響を及ぼすには時間や媒介物が必要ですが、量子もつれでは「なぜか一方を測ると、他方も即座に状態が決まる」ように観測されます。
このような現象は古典物理では説明できず、量子力学の独特な特徴とされています。
Q2. 実際に離れた場所で影響し合っているの?
A:
「影響している」とも「していない」とも言い切れません。というのも、量子もつれでは因果関係の伝達があるわけではないのです。
たとえば、2つのもつれた光子が地球と月に分かれていても、片方を測定するともう片方の結果が即座に決まるように見えます。しかしこれはあくまで統計的な相関にすぎず、情報の伝達や物理的な力の作用があるわけではありません。
このため、特殊相対性理論(光より速い通信はできない)とも矛盾しないとされています。
Q3. 量子もつれは通信に使えるの?
A:
直接的には使えません。
もつれた粒子を使っても、一方の測定結果を見ただけでは相手の情報がわからないからです。つまり、もつれは「相関関係」は作れても、「情報の送信」はできないのです。
ただし、量子通信の分野では、量子もつれを安全な鍵配送(量子鍵配送)に使う技術が発展しています。これは盗聴が原理的に不可能とされるため、将来のセキュア通信の基盤になると期待されています。
Q4. なぜ量子コンピュータで量子もつれが重要なの?
A:
量子コンピュータが非常に強力になる理由の1つが、量子もつれによる並列性です。複数の量子ビット(qubit)がもつれた状態になることで、個々のビットの単独処理ではなく、「全体としての計算状態」を操作できるようになります。
これは、古典的なコンピュータでは絶対に実現できない構造です。たとえば、もつれた100量子ビットは、2100 通りの状態を同時に扱えるポテンシャルを持つと言われます。
そのため、因数分解、最適化、量子化学計算などの分野で桁違いの計算能力が期待されているのです。
Q5. 量子もつれはいつか日常生活で使えるようになるの?
A:
すでに一部では実用化が始まっています。たとえば:
- 中国は量子暗号衛星「墨子号」により、長距離の量子鍵配送を実証済み
- 欧州や米国でも、量子インターネットの基盤技術としてもつれの応用が研究中
- 医療画像やセンシング分野でも、量子もつれを利用した「量子超解像技術」が検討されています
ただし、家庭やスマートフォンで使われるようになるにはまだ数十年単位の研究と開発が必要と見られています。





コメント